Unos haces proyectivos para la parábola

En 2017 publiqué en The College Mathematics Journal como una classroom capsule, el artículo Homographic Pencils for the Ellipse and the Hyperbola ¿Cómo no se me ocurrió en pensar algo parecido para la parábola? ¿Cómo el referee no me lo apuntó? 

Hasta hoy no se me ha ocurrido pensar en ello. Dedico esta entrada y este descubrimiento a la memoria de  nuestro amigo Ángel Montesdeoca, que falleció ya hace casi un año, pero no tuve conocimiento de ello hasta hace unos días.

Según el teorema de Chasles-Steiner, si tenemos una homografía $f:A^* \to B^*$ del haz de rectas que pasan por $A$ en el haz de rectas que pasan por $B$, y la homografía no es una siempre proyección, es decir,  cada recta y su imagen no se cortan todas en una misma recta, lo hacen en una cónica. 

Dados dos puntos $A$ y $B$, y un punto $V$ sobre la mediatriz de $AB$, buscamos la homografía $f:A^* \to B^*$ para la que la cónica correspondiente sea la parábola que pasa por $A$ y $B$ y que tiene vértice $V$.

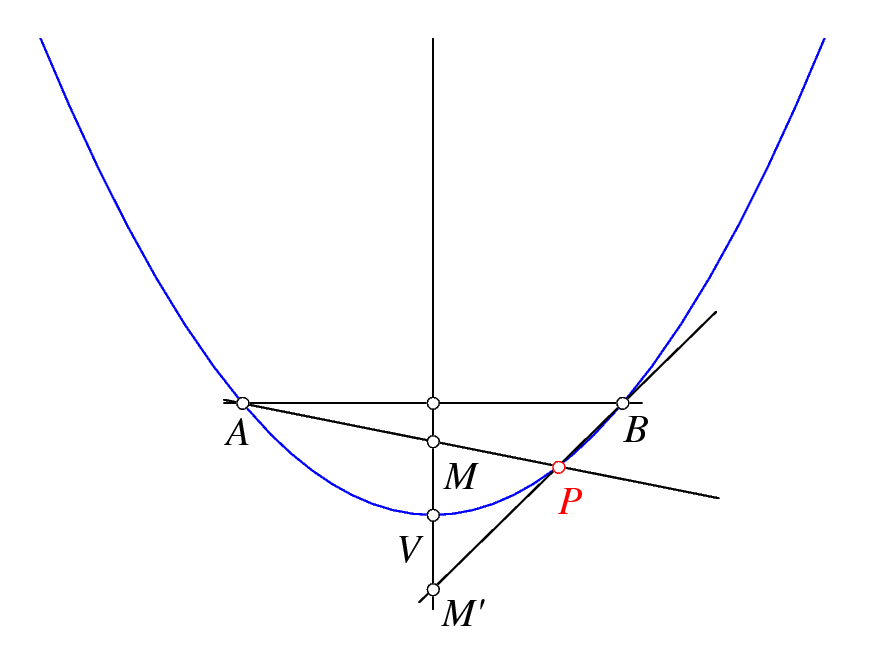
Como muestra la figura anterior, la homografía $f$ es muy sencilla: para cualquier $M$ sobre la mediatriz de $AB$, hallamos el simétrico $M'$ de $M$ respecto del vértice $V$ y entonces definimos $f(AM)=BM'$. 

Es facil comprobar que $AM$ y $BM'$ se cortan sobre la parábola que pasa por $A$ y $B$ y tiene vértice $V$. 

En  coordenadas  cartesianas  podemos  expresar  $A = (-a, 0)$, $B=(a,0)$, $V=(0,v)$, $M=(0,m)$ y $M'=(0,2v-m)$. Entonces se puede comprobar que las rectas $AM$ y $BM'$ se cortan en el punto $P = \left( {\frac{{a(v - m)}}{v},\frac{{m(2v - m)}}{v}} \right),$ que está sobre la parábola $a^2 y = v (a^2 - x^2)$.