Mutually Polar Triangles

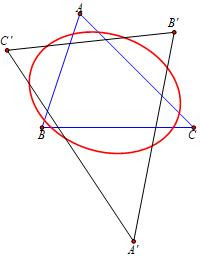
The main purpose of this document is to prove the following facts using barycentric coordinates:

Proposition 1. Given a reference triangle and a conic, there exists a triangle $A'B'C'$ such that $ABC$ and $A'B'C'$ are perspective and  mutua\-lly polar with respect to the conic. 

Proposition 2. Let $ABC$ be a triangle and $P$ a point. If $A'B'C'$ is a triangle with perspector $P$ there exists a conic such that $ABC$ and $A'B'C'$ are mutually polar with respect to the conic. 

Donwload; Mutually Polar Triangles

Un problema de lugar geométrico

Resolvemos de forma geométrica y de forma analítica el siguiente problema:

Dados tres puntos $A$, $B$, $C$ en este orden sobre una recta, hallar el lugar geométrico de las intersecciones de las tangentes trazadas desde los puntos $A$ y $C$ a las circunferencias tangentes en $B$ a la recta dada.

Descarga: Un problema de lugar geométrico

Analyzing a "Find the angle x" problem.

We solve a geometric problem of the kind "Find the angle x" by exploring the geometric constructions living in the problem and changing the point of view of it in order to discover the path from the statement to the solution. 

Descarga: Analyzing a "Find the angle x" problem