Existence of the triangle with sides $\sqrt{bc}$, $\sqrt{ca}$, $\sqrt{ab}$.

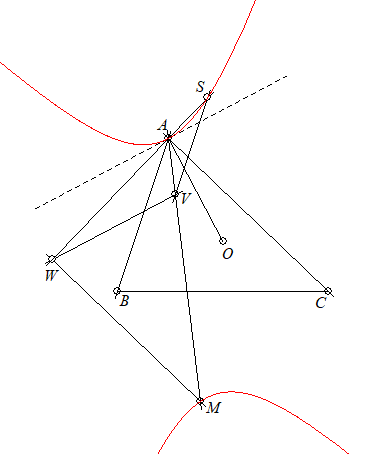
Given the sides $a$,$b$,$c$ of a rectangle we would like to know if a triangle exists whose sides are $\sqrt{bc}$, $\sqrt{ca}$, $\sqrt{ab}$, the geometric means of $a$, $b$, $c$. 

Descarga:
Existencia del triángulo con lados $\sqrt{bc}$, $\sqrt{ca}$, $\sqrt{ab}$

Construction of X5000 and X5001

We give a construction of points X5000 and X5001.

Construction of X5000 and X5001

The crosspoint

We study some loci related to the construction known as crosspoint of two given points. The main result is as follows:

Let $ABC$ a triangle, $P$ a point and $L$ the trilinear polar of some point $M$. Then the locus of points $Q$ for which the crosspoint of $P$ and $Q$ lies on $L$ is the conic with perspector the crosspoint of  $P$ and $M$.

See details at The crosspoint

A property of X7090 and X14121

Given a triangle ABC, their points X7090 and X14121 are the complement of X176 and X175 respectively.

They are the centers of the circles tangent internally to the three circles with BC, CA, AB as diameters.

See details at A property of  X7090 and X14121

An insanely huge locus!

A problem proposed by Thanos Kalogerakis leads to an insanely huge locus: an algebraic curve of the 30th degree whose equation occupies more than 16500 pages!

Read: An insanely huge locus!

Attachment: Source code and equation of the locus

El número 6174

Presentamos esta conocida propiedad del número 6174 acompañándolo todo con algunas instrucciones del programa Mathematica.

Descarga: 6174.pdf

Un Problema de Silver Samuel Palacios Paulino

Descarga: Un Problema de Silver Samuel Palacios Paulino

Sum of ratios into hyperbola

We generalize a relation involving ratios proposed by Thanos Kalogerakis and find a hyperbola as locus. We construct the hyperbola by using Pascal theorem and find other formulas.

Sum of ratios involving ratios

Another construction of an inconic with given perspector

Given a point $P$ with cevian triangle $A'B'C'$ we construct two extra points $M, N$ lying on the inconic tangent to $BC$, $CA$, $AB$ at $A', B', C'$ respectively.

Another construction of an inconic with given perspector

Sum of digit powers

Sum of digits powers

Four points on Euler Line

I introduce  four new points on Euler line:

I found these points trying to solve a problem proposed by Kadir Altintas.

Given a triangle ABC and a point P, call DEF its circuncevian triangle. The circumcenters of six triangles PBD, PDC, PCE, PEA, PAF and PFB lie on the same conic. When this conic is a circle?

Updated March, 1. Additions/corrections are in red.

Four points on Euler line