http://garciacapitan.epizy.com
De vez en cuando uso la resultante de dos polinomios y el discriminante de un polinomio para resolver rápidamente con Mathematica alguna cuestión de tangencias. En el siguiente documento echamos un vistazo a estos dos conceptos.
La resultante y el discriminante
Given a triangle $ABC$ and two points $P$ and $Q$, it is well known that there are four conics through the two points and tangent to the three sidelines of $ABC$. For a projective construction, see Ángel Montesdeoca website.
Here we give a vision with barycentric coordinates (thanks to Ercole Suppa for his collaboration).
We give some properties of the so called bianticevian conic.
Download: The Bianticevian conic
Video (Spanish):
This time we study the following problem, proposed by David Nguyen in Facebook.
En 2017 publiqué en The College Mathematics Journal como una classroom capsule, el artículo Homographic Pencils for the Ellipse and the Hyperbola ¿Cómo no se me ocurrió en pensar algo parecido para la parábola? ¿Cómo el referee no me lo apuntó?
Hasta hoy no se me ha ocurrido pensar en ello. Dedico esta entrada y este descubrimiento a la memoria de nuestro amigo Ángel Montesdeoca, que falleció ya hace casi un año, pero no tuve conocimiento de ello hasta hace unos días.
Según el teorema de Chasles-Steiner, si tenemos una homografía $f:A^* \to B^*$ del haz de rectas que pasan por $A$ en el haz de rectas que pasan por $B$, y la homografía no es una siempre proyección, es decir, cada recta y su imagen no se cortan todas en una misma recta, lo hacen en una cónica.
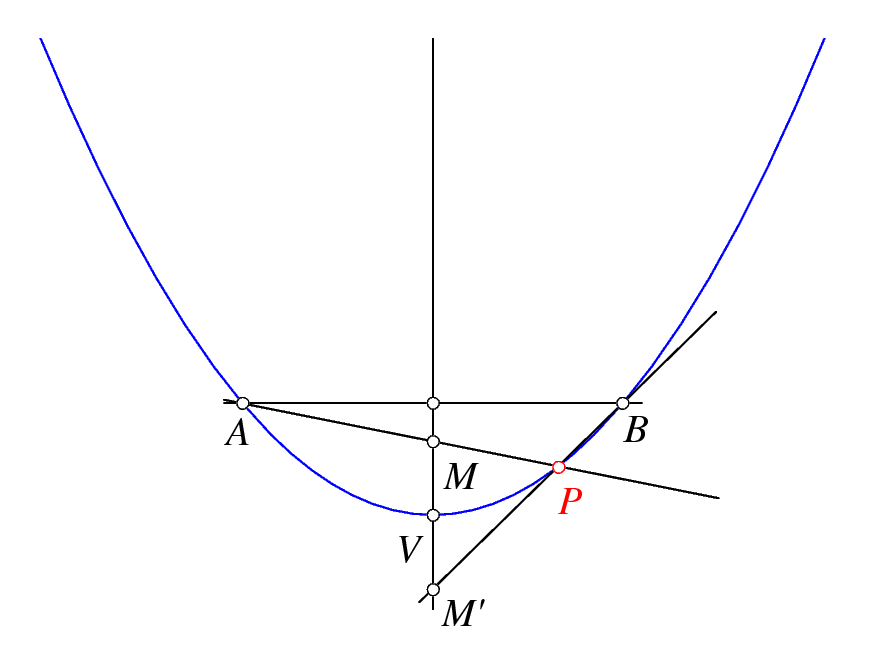
Dados dos puntos $A$ y $B$, y un punto $V$ sobre la mediatriz de $AB$, buscamos la homografía $f:A^* \to B^*$ para la que la cónica correspondiente sea la parábola que pasa por $A$ y $B$ y que tiene vértice $V$.
Como muestra la figura anterior, la homografía $f$ es muy sencilla: para cualquier $M$ sobre la mediatriz de $AB$, hallamos el simétrico $M'$ de $M$ respecto del vértice $V$ y entonces definimos $f(AM)=BM'$.
Es facil comprobar que $AM$ y $BM'$ se cortan sobre la parábola que pasa por $A$ y $B$ y tiene vértice $V$.
En coordenadas cartesianas podemos expresar $A = (-a, 0)$, $B=(a,0)$, $V=(0,v)$, $M=(0,m)$ y $M'=(0,2v-m)$. Entonces se puede comprobar que las rectas $AM$ y $BM'$ se cortan en el punto $P = \left( {\frac{{a(v - m)}}{v},\frac{{m(2v - m)}}{v}} \right),$ que está sobre la parábola $a^2 y = v (a^2 - x^2)$.
